Article novembre 2025
Rappels mathématiques
Une masse m, oscillant suivant un mouvement vibratoire sinusoïdal constitue un exemple d'oscillateur harmonique. Une particule oscille quand elle se déplace périodiquement autour d'une position d'équilibre. Le mouvement d'un pendule, une masse suspendue à un ressort, les atomes dans un solide, sont des exemples de mouvements oscillatoires.
On s'intéressera ici au mouvement sinusoïdal.
Si l'on prend l'exemple d'une masse reliée à un ressort horizontal de raideur k, sans frottement, l'équation du mouvement s'écrit : $ \vec{F} = m \vec{a} $. Si la direction d'oscillation est l'axe Ox, la force de rappel est proportionnelle et opposée au déplacement :
$ m \dfrac{d^2x}{dt^2} = -k x \quad \Rightarrow \quad \dfrac{d^2x}{dt^2} + \omega^2 x = 0 \quad avec \quad \omega^2 = \dfrac{k}{m} $
Cette équation est idéale pour illustrer les principes de résolution d'équations différentielles ordinaires (EDO) et les méthodes numériques / apprentissage de dynamiques.
La solution générale de cette équation différentielle est de type :
$ x(t) = A cos(\omega t) +B sin (\omega t) $
où A et B sont des constantes à déterminer.
Pour déterminer la constante A, on applique la condition initiale :
à t = 0, $ x(0) = A = x_0 $
Pour déterminer la constante B, on applique la condition initiale de vitesse :
$ \dot{x}(t) = -A \omega sin(\omega t) +B \omega cos (\omega t) $
à t = 0, $ \dot{x}(0) = B \omega = v_0 \quad \Rightarrow \quad B = \dfrac{v_0}{\omega} $
Les équations sont :
$ x(t) = x_0 cos(\omega t) +\dfrac{v_0}{\omega} sin (\omega t) $
et
$ \dot{x}(t) = \dfrac{dx}{dt} = -x_0 \omega sin(\omega t) +v_0 cos (\omega t) $
Génération de données
Avant de passer à l'apprentissage à l'aide des réseaux de neurones, générons d'abord des données numériques à partir de notre équation différentielle. Cela nous permettra de disposer d'un jeu de référence pour comparer les résultats obtenus par les modèles de type Neural ODE et PINN (Physics-Informed Neural Network).
Voici un exemple de code de génération de données de l'oscillateur harmonique à l'aide de solve_ivp (SciPy) :
import numpy as np
from scipy.integrate import solve_ivp
omega = 2.0 # pulsation propre
t_eval = np.linspace(0, 10, 500)
def osc_harmonique(t, y):
x, v = y
return [v, -omega**2 * x]
# condition initiale
y0 = [1.0, 0.0]
sol = solve_ivp(osc_harmonique, (0, 10), y0, t_eval=t_eval)
x, v = sol.y
Une fois les données simulées, nous pouvons entraîner un modèle neuronal à reproduire la dynamique observée. On commence par la première approche : les Neural ODEs, où l'équation différentielle elle-même est paramétrée par un réseau.
Entraînement du modèle neuronal : approche Neural ODE
L'idée d'une Neural Ordinary Differential Equation (Neural ODE) est de représenter directement la loi d'évolution d'un système dynamique par un réseau de neurones.
Convergence de l'apprentissage
Après environ 1800 itérations d'entraînement, la fonction de perte atteint une valeur d'environ 3x$10^{-3} $, traduisant une bonne convergence du modèle. Le réseau neuronal a ainsi appris à reproduire fidèlement la dynamique du système différentiel :
$ \dfrac{d^2x}{dt^2} = - \omega^2 x $
Sans connaître cette équation, le modèle a su identifier la loi de mouvement à partir des seules données de trajectoire.
Visualisation du résultat
Le graphique ci-dessous montre la comparaison entre la solution analytique (pointillée) et la prédiction du Neural ODE (trait rouge).
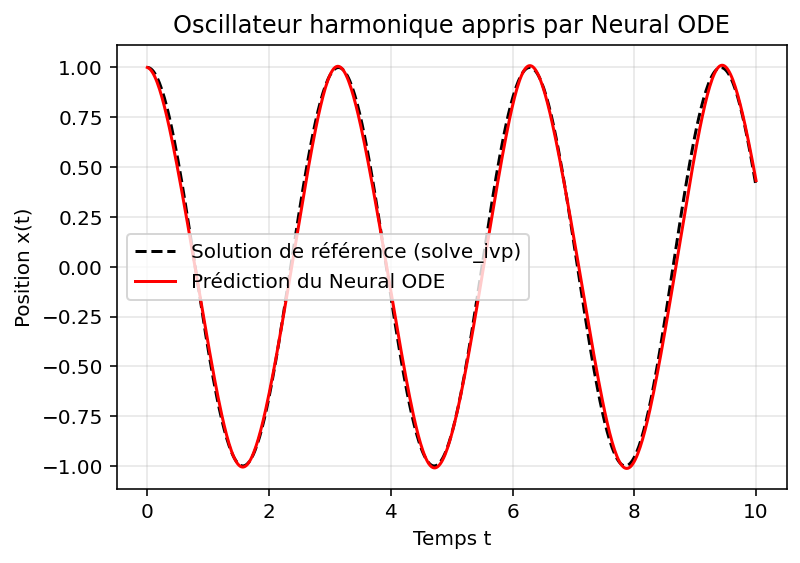
Figure 1 - Le tracé rouge suit parfaitement la sinusoïde de référence, confirmant que le modèle
a capturé la structure oscillatoire du système.
Interprétation des résultats
- La faible valeur finale de la loss ($ \sim $ 3 x $10^{-3} $) indique que la fonction $ f_\theta (x, t) $ apprise par le réseau approxime très bien le champ de vitesse réel $ f(x,t) = (v, -\omega^2x) $.
- La forme sinusoïdale du signal prédit montre que le modèle a intégré la périodicité naturelle du mouvement.
- Contrairement à un réseau classique qui apprend seulement à prédire les positions successives, le Neural ODE apprend directement la loi du mouvement elle-même. Autrement dit, il comprend comment le système évolue en continu dans le temps, et pas seulement une suite de points discrets.
Apprentissage des lois physiques avec les Physics-Informed Neural Networks (PINNs)
Ces modèles combinent les outils du deep learning avec les équations différentielles connues du système.
Les PINNs permettent d'intégrer directement les équations de la physique dans l'apprentissage d'un réseau neuronal. Plutôt que d'apprendre uniquement à partir de données, le réseau est guidé par les équations différentielles qui régissent le système. Dans cet exemple, on applique un PINN à un oscillateur harmonique simple, défini par :
$ \dfrac{d^2x}{dt^2} + \omega^2 x = 0 $
Implémentation en PyTorch
- On crée un réseau avec nn.Sequential.
- On calcule sa dérivée première et seconde avec torch.autograd.grad.
- On définit une fonction de perte composée de deux parties :
- une loss de données (optionnelle, si on a des points observées),
- une loss physique (résidu de l'équation différentielle).
Principes et apprentissage
Le réseau $ x_\theta (t) $ cherche à approximer la solution de l'équation tout en respectant la physique du problème. Sa fonction de perte combine deux termes :
1. Le résidu physique, qui mesure à quel point le réseau respecte l'équation différentielle :
$ L_{phys} = \left\|\dfrac{d^2x_\theta}{dt^2} + \omega ^2 x_\theta \right \|^2 $
$ L_{ic} = (x_\theta(0) - 1)^2 + ( \dot{x}_\theta (0) ) ^2 $
$ L = L_{phys} + L_{ic} $
Résultats et interprétation
Après l'entraînement, la courbe rouge (prédiction PINN) se superpose parfaitement à la solution analytique (courbe noire pointillée). Cela montre que le réseau a intégré la loi physique directement dans son apprentissage, sans nécessiter de grands volumes de données d'entraînement.
Contrairement aux Neural ODEs qui apprennent la dynamique à partir de données, les PINNs apprennent à respecter la physique elle-même.
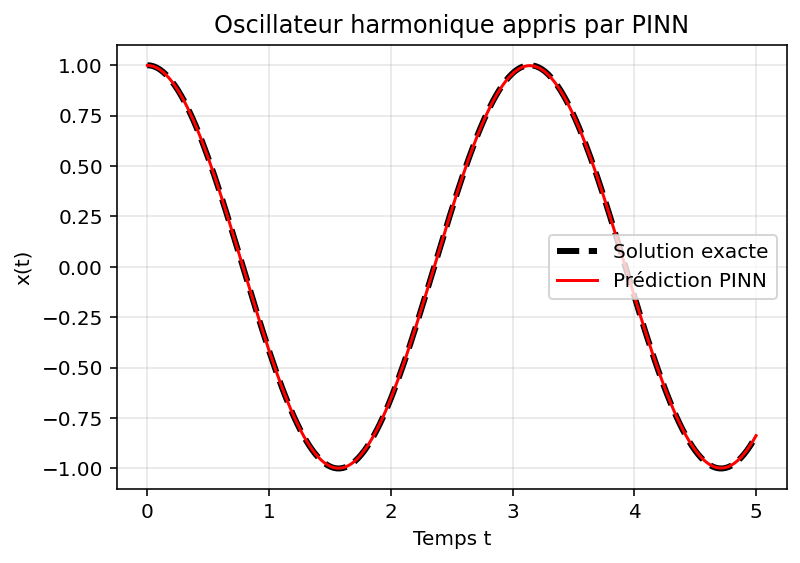
Figure 2 - Résultats de l'entraînement du Physics-Informed Neural Network (PINN) sur l'oscillateur harmonique. La courbe rouge (prédiction du modèle) coïncide avec la solution analytique (courbe noire), confirmant que le réseau satisfait l'équation $ \dfrac{d^2x}{dt^2} + \omega^2 x = 0 $ et les conditions initiales $\ x(0) = 1, \dot{x} (0) = 0 $. La prédiction suit la sinusoïde de référence, montrant que le modèle respecte bien la contrainte physique imposée dans le fonction de perte. Contrairement au Neural ODE, le PINN intègre la physique dès la phase d'apprentissage, garantissant des solutions cohérentes même avec peu de données observées.
Ce bon comportement du modèle sur un système linéaire simple nous permet maintenant de passer à un cas beaucoup plus complexe : le système chaotique de Lorenz (découvrir ici).